Loading... ## 0x00 $\mathcal{O}(n^3)$ 预处理 $\mathcal{O}(n)$ 查询 这种大量查询的题目很容易想到的是预处理出来每一对 $\operatorname{dis}(x, y)$ 。这样在查询的时候就可以 $O(n)$ 查询出来,并且求出答案。具体实现可以这样做:由于“ $\operatorname{dis}(x, y)$ 为 $x,y$ 两点之间唯一简单路径上边权的异或和。”很显然的是,对这个无根树选定一个根节点,这条简单路径还是原来的简单路径,那么 $O(1)$ 求出 $x,y$ 的 lca 节点,暴力跑一遍路径进行计算即可。 ## 0x01 $\mathcal{O}(n^2)$ 预处理 $\mathcal{O}(n)$ 查询 对于 0x00 部分的算法,可以进行优化,首先预处理把每一个对 $\operatorname{dis}(x, y)$ 时间复杂度不会变化,那么 $\mathcal{O}(1)$ 求出 $x,y$ 的 lca 节点后,希望可以 $\mathcal{O}(1)$ 求出 $\operatorname{dis}(x, y)$ ,考虑这里 $\operatorname{dis}(x, y)$ 若不是“路径上边权的异或和”而是“路径上边权的和”,可以使用树上前缀和,那么异或和也可以采用这样的方法,处理出每一个节点到根节点的异或和,参见下面一个图: 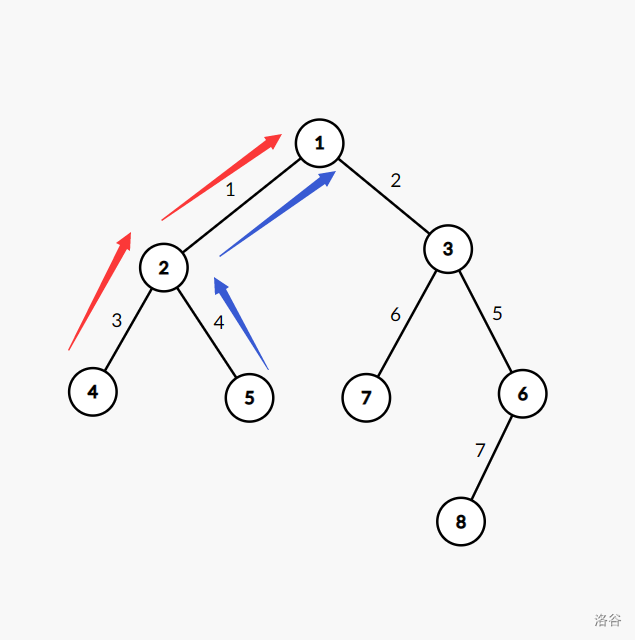 对于 $\operatorname{dis}(4, 5)$ 已知 $\operatorname{dis}(1, 4) = 1 \oplus 3$ 和 $\operatorname{dis}(1, 5) = 1 \oplus 4$ 这两个信息重复的部分即为 $\operatorname{dis}(1, 2) = 1$ ,但是由于异或的自反性质,直接讲这两部分异或起来就去除了 $\operatorname{dis}(1, 2) = 1$ 这部分,即为 $\operatorname{dis}(1, 5) \oplus \operatorname{dis}(1, 2) = 3 \oplus 4 \oplus 1 \oplus 1 = 3 \oplus 4$ 。那么就可以做到 “$\mathcal{O}(n^2)$ 预处理 $\mathcal{O}(n)$ 查询” 。 ## 0x02 $\mathcal{O}(n)$ 预处理 $\mathcal{O}(1)$ 查询 刚才的算法打开了一个很好的思路就是利用了异或的自反性,希望还可以利用更多这样的性质,这时整体考虑 $$ \operatorname{val}_{x, y}(i) = \operatorname{dis}(x, i) \oplus \operatorname{dis}(y, i)\\ = \operatorname{dis}(x, 1) \oplus \operatorname{dis}(i, 1) \oplus \operatorname{dis}(y, 1) \oplus \operatorname{dis}(i, 1) \\ = \operatorname{dis}(x, 1) \oplus \operatorname{dis}(y, 1) $$ 可以发现 $ \operatorname{val}_{x, y}(i) $ 和 $i$ 没关系,那么对于 $\displaystyle \bigoplus_{i = l}^{r} \operatorname{val}_{x, y}(i)$ 也就是 $\displaystyle \bigoplus_{i = l}^{r} \operatorname{dis}(x, 1) \oplus \operatorname{dis}(y, 1) $ ,相当于自己和自己异或了 $r-l+1$ 次,更具自反性质得到 $r-l+1\bmod 2 = 1$ 时为 $\operatorname{dis}(x, 1) \oplus \operatorname{dis}(y, 1) $ ,否则为 $0$ 。 ```cpp #include <cstdio> #include <algorithm> #include <queue> #define _min(a,b) ((a)<(b)?(a):(b)) #define _max(a,b) ((a)>(b)?(a):(b)) struct edge{ int to,nxt,w; edge(){ nxt=-1; return; } }tree[1000010<<1]; int tot,head[1000010]; long long V_pre[1000010]; void addEdge(int u,int v,int w){ tree[tot].nxt=head[u]; tree[tot].w=w; tree[tot].to=v; head[u]=tot; ++tot; return; } int read(){ long long x=0;char f=0,c=getchar(); while(c<'0'||'9'<c) f|=(c=='-'),c=getchar(); while('0'<=c&&c<='9') x=(x<<1)+(x<<3)+(c&15),c=getchar(); return f?-x:x; } void dfs(int u,int p,int w){ V_pre[u]=V_pre[p]^w; for(int i=head[u];~i;i=tree[i].nxt){ if(tree[i].to!=p) dfs(tree[i].to,u,tree[i].w); } } int main(){ register int i,u,v,w,x,y,l,r; register long long ans; int n=read(); int Q=read(); for(i=1;i<=n;++i) head[i]=-1; for(i=1;i<n;++i){ u=read(); v=read(); w=read(); addEdge(u,v,w); addEdge(v,u,w); } dfs(1,1,0); for(i=0;i<Q;++i){ x=read(); y=read(); l=read(); r=read(); ans=(((r-l+1)&1)?(V_pre[x]^V_pre[y]):0); printf("%lld",ans); putchar('\n'); } return 0; } ``` 最后修改:2023 年 11 月 10 日 © 允许规范转载 赞 如果觉得我的文章对你有用,使用点这里使用虚拟货币进行赞赏