Loading... ## 前言 本文宗旨解释一下斜率优化本质问题,而不是表面上的讲解一个模板,本文可以作为一个较为权威的资料参考学习,但不建议直接使用本材料第一次学习斜率优化,这样只是知识的灌输,而没有思考。 ## 前置知识 1. DP 2. 平面直角坐标系 3. 直线解析式 4. 凸包 递增指的是,对于一个序列任 $S$ 有: $s_i,s_j\forall S \cup i < j,s_i \leq s_j$ ;同理定义递减 $s_i,s_j\forall S \cup i < j,s_i \geq s_j$ 。 在本文中,凸多边形是指所有内角大小都在 $\left[0,\pi\right]$ 范围内的简单多边形。 下凸壳就是对于按照x轴排序的的点,前一个点和后一个点的直线斜率从 $\left[-\infty,\infty\right]$ 单调递增。 上凸壳就是对于按照x轴排序的的点,前一个点和后一个点的直线斜率从 $\left[\infty,-\infty\right]$ 单调递增。 一条直线对于 $X$ 轴的截距指的是其常数项的大小(可能为负) 。 ## 正文 ### 斜率优化适用范围 斜率优化dp,这个dp自然需要转移方程,将这个dp转移方程化为一个多项式形式,那么只有满足这样的多项式转移方程才能适用斜率优化: $$ dp_i=\min_{j\in set_i}\left(Y_j+K_i\times X_j+B_i\right) $$ 或者 $$ dp_i=\max_{j\in set_i}\left(Y_j+K_i\times X_j+B_i\right) $$ 这里我们先看 $\min$ 的情况。这个式子在求解 $i$ 这个状态的答案,而 $j$ 相当于在能对 $dp_i$ 贡献的状态中进行枚举,对于其中 $Y_j,K_i,B_i$ 三个函数,分别只与其自变量相关,即只与 $j,i,i$ 相关,并且已知 $K_i,B_i$ ,这时找到一个 $j$ 使其和最小即可转移。 这个程序的时间复杂度容易分析 $\mathcal{O}\left(\sum_{i=1}^{n}|set_i|\right)$ ,其中n并不一定是所有的状态数,由于dp本质是DAG,那么我们对于这个包含最终答案的联通块进行拓扑排序,形成一个求解顺序,n就是最少可以求解的状态数量。 对于这个式子考虑对于每一次求解进行优化,期望可以得到 $\mathcal{O}\left(1\right) \text{ or } \mathcal{O}\left(\log|set_i|\right)$ 的世间复杂度,那么总体时间复杂度就会减小很多,极其接近于 $\mathcal{O}\left(n\right)$ 的时间复杂度。 考虑可以对这个式子进行移项: $$ dp_i-K_i\times X_j-B_i=Y_j $$ 这个式子的每一组取值就是关于这个状态的一种转移方式,所以我们舍去 $\min$ 来看,但是这样看着麻烦,重新定义一下 $K_i,B_i$ 写成这样: $K_i\times X_j+B_i+dp_i=Y_j$ 发现这个式子可以看成一个直线解析式,其中已知了斜率 $k$ ,并且 $B_i+dp_i$ 一起作为了这条直线和y轴的截距,而不是只是 $B_i$ ,而且由于这个dp式子要有意义,也就是要是一个真实存在的一个转移,那么 $X_j$ 和 $Y_j$ 必须是一个存在的值才行,考虑在考查每一个 $j$ 的时候,就已知了 $X_j$ 和 $Y_j$ ,把 $\left(X_j,Y_j\right)$ 看做一个点,相当于这条直线过了这个点,即可解出 $dp_i$ ,要使得 $dp_i$ 尽量小,而 $B_i$ 在求解这个状态中始终不变,那么要使这个直线和y轴的截距就要尽量小。那么这条这时问题就变成,找到一个点,使得这条直线截距(这里的)最小。 举个例子,对于下图这些点,随机取几个斜率范围在 $\left[-\infty,\infty\right]$ ,并且求解到最小值,能取到的点像这样: 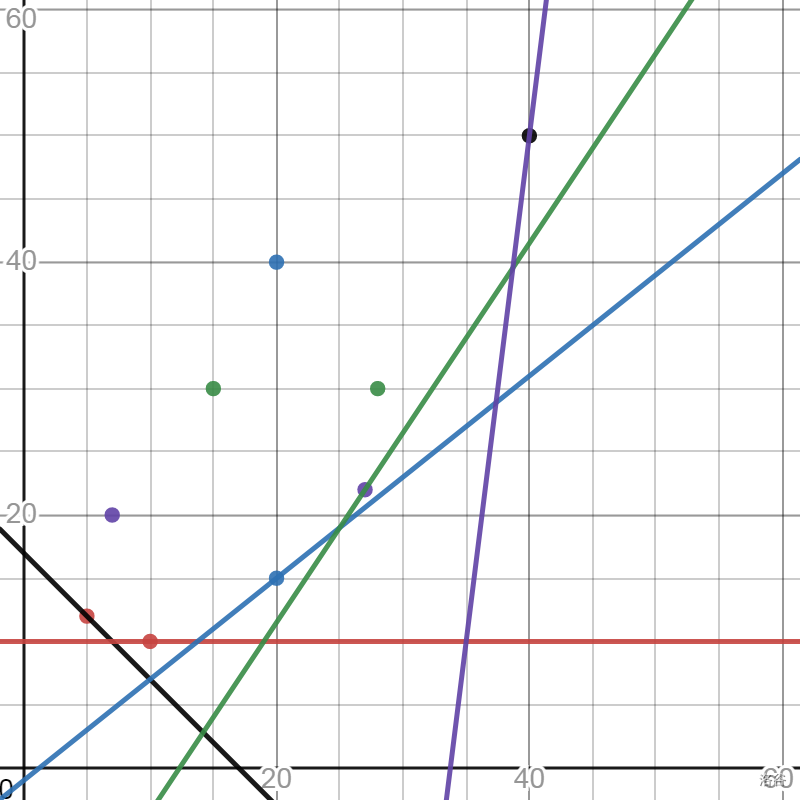 实际上维护的就是一个下凸壳,显然其他的点都是没用的,下图是要维护的点集: 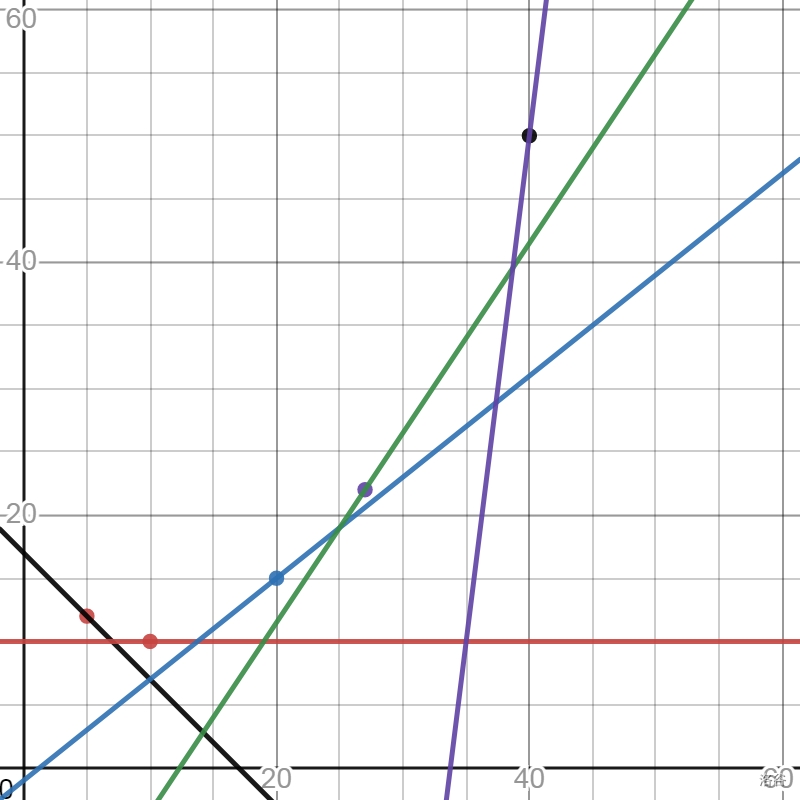 同理如果是 $\max$ 则是维护上凸壳。 ### 特殊斜率优化 大多数情况中我们都是在顺序求解 $dp_i$ ,对于解集也是顺序插入每一个 $j$ ,而不是在一个DAG中使用拓扑排序顺序求解。 #### $X$ 和 $Y$ 均有单调性 / 线性数据结构维护 队列情况: | | 斜率递增 | 斜率递减 | | ----- | -------------- | -------------- | | X递增 | min/维护下凸壳 | max/维护上凸壳 | | X递减 | max/维护上凸壳 | min/维护下凸壳 | 这些情况下都可以使用单调队列维护。以斜率递增并且 $X$ 递增的情况来说。 对于每次放入一个点到点集的时候,将其放入对头,但是这样可能破坏下凸壳性质,所以要一直从对头弹出点,直到符合下凸壳性质,显然这些弹出的点以后永远不会成为更优解; 例如下图,加入了橙色点,橙点和紫点的直线斜率小于黑点和紫点的直线斜,显然黑点破坏了下凸壳性质,那么弹出黑点,显然这样可以使以后求解更优。 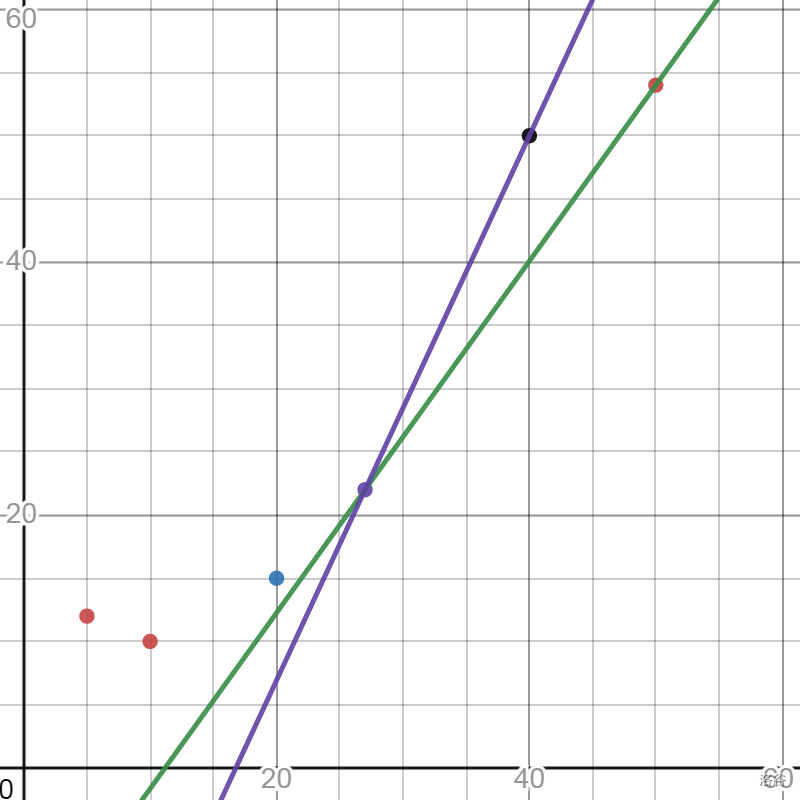 在求解取点的时候我们从队尾不断弹出点,直到队尾两个点的斜率大于当前直线,由于斜率递增,显然这些点以后永远不能成为更优解,这时队尾的点就是最优解。 栈的情况: | | 斜率递增 | 斜率递减 | | ----- | -------------- | -------------- | | X递增 | max/维护下凸壳 | min/维护上凸壳 | | X递减 | min/维护上凸壳 | max/维护下凸壳 | 这种时候处理和队列处理相似,对于加入新点,不断弹出栈顶的点使得其符合上凸壳性质,由于斜率递增,那么这些弹出的点永远不会成为更优解;对于求解取点,我们在栈顶不断弹出点使得栈顶两个点的斜率大于当前直线斜率,由于斜率递增,那么这些弹出的点永远不会成为更优解,这时栈顶的点显然是最优解; 小结:由于 $X$ 单调性的所以可以顺序将求出的点放入队列/栈中就可以维护一个按照 $X$ 递增的点集;由于 $K$ 单调性,那么我们可以弹出一些永远不会成为最优解的点,这样对于每个点最多入队/入栈和出队/出栈一次,故时间复杂度是 $\mathcal{O}(n)$。 #### $X$ 有单调性 / 线性数据结构维护 由于 $X$ 有单调性我们还是能用线性数据结构存储,因为只会在一头插入不会在中间插入;但由于 $K$ 没有单调性,那么我们就会面临在中间查找一个点的情况,又因为点集中斜率是单调递增的,并且具有连续存储的性质,我们可以二分查找一个点使得斜率最接近这条直线就是最优解。故时间复杂度是 $\mathcal{O}(n\log n)$。 #### 其余情况 由于 $X$ 没有单调性,那么我们就会面临在中间插入/删除点的情况,又要在中间查找一个点,那么不难想到使用平衡树进行维护点集。 ### 多维斜率优化 $$ dp_{i,j}=\min_{(k,l)\in set_i}\left(Y_{k,l}+K_{i,j}\times X_{k,l}+B_{i,j}\right) $$ 行如这样的多维斜率优化可以考虑划归为一维的情况处理,化为行如这样的形式: $$ dp_{i+n\times j}=\min_{(k+n\times l)\in set_i}\left(Y_{k+n\times l}+K_{i+n\times j}\times X_{k+n\times l}+B_{i+n\times j}\right) $$ 这个东西可以扩展到n维的斜率优化。 但是这样还是未免有些麻烦,但是对于一些特殊情况我们仍然又一些trick使得求解更简单,例如: $$ dp_{i,j-1}=\min_{(k,j-1)\in set_i}\left(Y_{k,j-1}+K_{i,j}\times X_{k,j-1}+B_{i,j}\right) $$ 这时我们可以参考滚动数组的方法处理,每一层也就是每一个 $i$ 求解后记录下来,下层求解使用上次记录的数即可,然后滚动记录覆盖。 ## 附录 ### 叉积判断斜率 由于需要斜率判断,对于两个 $P,Q$ 点的斜率。我们使用斜率公式计算 $\frac{Y_P-Y_Q}{X_P-X_Q}$ 但是这样计算需要浮点数,非常有可能爆精度。我们可以换一种方式计算,实际上在正式应用中我们大多数时候是在计算两个斜率的大小关系,假设有 $A,B,C,D$ 四个点,假设有个表达式(当然这个表达式可能为假) $K_{A,B}<K_{C,D}$ 那么则有 $\frac{Y_A-Y_B}{X_A-X_B}<\frac{Y_C-Y_D}{X_C-X_D}$ 如果 $X_A-X_B,X_C-X_D$ 同号的情况下则有 $\\left(Y_A-Y_B)*\left(X_C-X_D\right)<\left(Y_C-Y_D\right)\left(X_A-X_B\right)$ 这样就可以避免精度问题,但是一定注意不等式符号变化问题。 ### 上/下凸壳维护点集正确性证明 在前面的过程中,我们直观感受了在函数图像中能去到最优解的点是一个凸壳,但是缺乏严谨的证明。这里以下凸壳取最小做证明。 定义一个点 $P\left(X_P,Y_p\right)$ 下凸壳在上方表示:对于这个点集按照 $X$ 递增排序,第一个点是 $\left(X_1,Y_1\right)$ 最后一个点是 $\left(X_n,Y_n\right)$ 。对于这 $P$ 点有, $X_1\leq X_P \leq X_n$ ,并且 $P$ 在这个下凸壳中每两个相邻点的直线的上方。 我们发现在维护下凸壳时我们会弹出一些点,而这些点都是在这个下凸壳上方,证明:设 $A\left(X_A,Y_A\right)$ 这个点我们找到在 $X$ 轴上距离最近两个 $P\left(X_P,Y_P\right)$ 和 $Q\left(Q_P,Q_P\right)$ 并且 $P$ 在 $Q$ 左侧,由于 $A$ 在这个下凸壳上方所以 A 在直线 $l_{PQ}$ 上方,并且在线段 $PQ$ 上方,易证 $k_{PA} > k_{AQ}$ 。 那么进而我们可以发现在 $A$ ,在这条直线上方,所以一条求解时某条直线去到 $A$ 点到 $X$ 轴的截距会更大(在 $PQ$ 上方显然截距更大) 。 并且可以发现用线性数据结构维护点集时,用斜率弹出的点都是在下凸壳上方的点。 小结:由于在下凸壳上方的点都会破坏下凸壳性质,剩下的点都是下凸壳点集的点,而下凸壳上方的点不会成为更优解,所以维护下凸壳可以找到最优解。 ### WQS二分 套上 斜率优化 关于WQS二分详情见"[附1:WQS二分简述](https://www.luogu.com.cn/blog/zi-gao/wqs-er-fen-jian-shu)"。这里如果一个斜率优化限制转移 $a$ 次,可以考虑使用WQS二分,这里只需要将 $\operatorname{f}\left(x\right)$ 计算的式子套上斜率优化即可,并且注意这时的转移方程应该是 $dp_i=Y_j-K_iX_j-mid$ 。算法所以主体是WQS二分,斜率优化。 ### 例题 请读者按照顺序做,层层递进的题目编排。 1. [P3195 [HNOI2008]玩具装箱](https://www.luogu.com.cn/problem/P3195) 2. [P5017 [NOIP2018 普及组] 摆渡车](https://www.luogu.com.cn/problem/P2305) 3. [P2365 任务安排](https://www.luogu.com.cn/problem/P2365) 4. [P3628 [APIO2010] 特别行动队](https://www.luogu.com.cn/problem/P3628) 5. [P2120 [ZJOI2007] 仓库建设](https://www.luogu.com.cn/problem/P2120) 6. [P5785 [SDOI2012]任务安排](https://www.luogu.com.cn/problem/P5785) 7. [P4072 [SDOI2016]征途](https://www.luogu.com.cn/problem/P4072) 8. [P4360 [CEOI2004] 锯木厂选址](https://www.luogu.com.cn/problem/P4360) 9. [P2305 [NOI2014] 购票](https://www.luogu.com.cn/problem/P2305) 10. [P5308 [COCI2018-2019#4] Akvizna](https://www.luogu.com.cn/problem/P5308) 题解在"[附2:题目浅析](https://www.luogu.com.cn/blog/zi-gao/ti-mu-qian-xi)"中。 最后修改:2023 年 11 月 10 日 © 允许规范转载 赞 如果觉得我的文章对你有用,使用点这里使用虚拟货币进行赞赏
1 条评论
我喜欢MuC,大佬能教我怎么追吗?